Grid paintings à la Mondrian with JavaScript
I was at a laundrette today and had just finished my book so I had some time to kill. Naturally I devised an algorithm for generating drawings that would resemble the grid-like paintings that Piet Mondrian made famous. With the benefit of hindsight I guess I could indulge in saner activities while waiting for my laundry to dry!
I went through different ideas but in the end I settled on a recursive approach. My idea is to divide a rectangle into two smaller ones and then to do the same with each sub-rectangle. Every time a rectangle is generated and is then filled with a random color; like Mondrian I use yellow, red, blue, black and white.
The work
In the end the algorithm I implemented generates images like these.
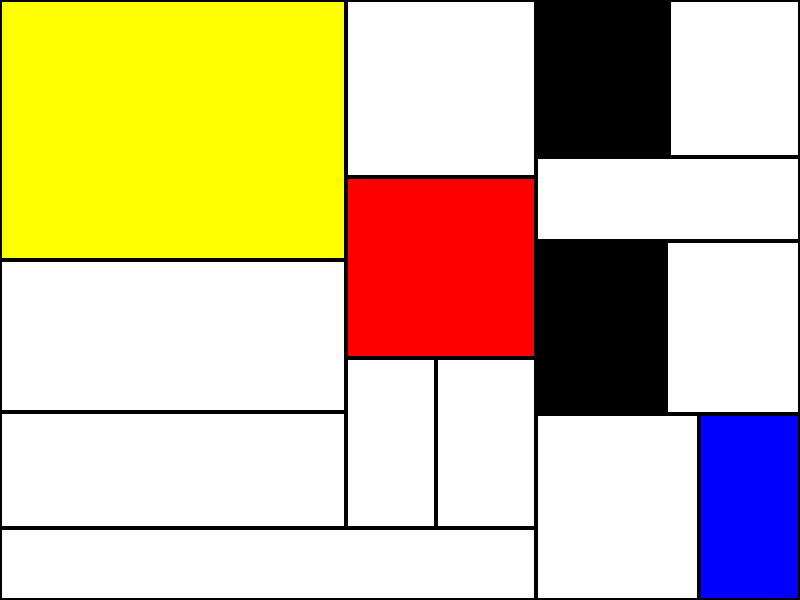
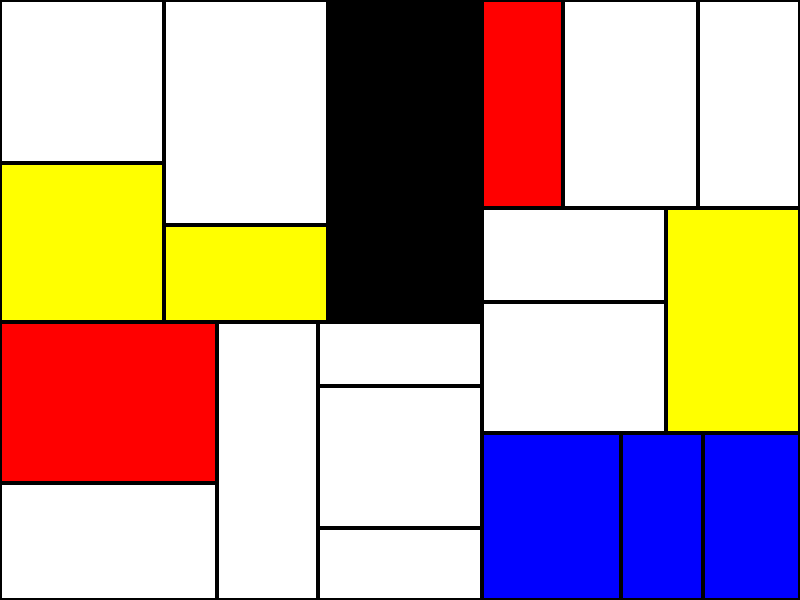
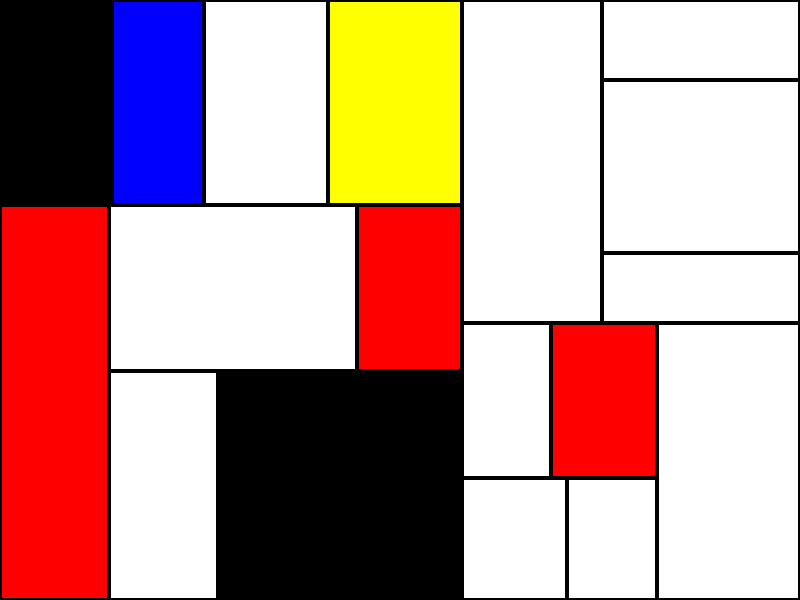
The code
The implementation is very short. I started by defining two classes - Point and Rectangle - for the sake of tidiness.
class Point {
constructor(x, y) {
this.x = x;
this.y = y;
}
}
class Rectangle {
constructor(min, max) {
this.min = min
this.max = max
}
get width() {
return this.max.x - this.min.x
}
get height() {
return this.max.y - this.min.y
}
}
A rectangle is thus defined by an upper left point - called min - and a lower right point - called max. Here is an image just to make things clear.

The next step is to be able to draw a rectangle. The CanvasRenderingContext2D has a strokeRect(x1, y1, x2, y2) method but I had already written something before I knew this; anyway it isn’t very complicated. I attached the method to the Rectangle class.
class Rectangle {
draw(ctx) {
ctx.moveTo(this.min.x, this.min.y)
ctx.lineTo(this.max.x, this.min.y)
ctx.lineTo(this.max.x, this.max.y)
ctx.lineTo(this.min.x, this.max.y)
ctx.lineTo(this.min.x, this.min.y)
}
}
I simply go around each corner of the rectangle in a clockwise fashion, starting at the top-left corner.

Kid’s stuff! Now comes the interesting part. The next step is to split a rectangle in two; there are two pitfalls to handle:
- A rectangle can be half in two ways, either left/right or either top/bottom.
- A split can produce rectangles which are too narrow and not visually appealing.
To handle the first pitfall, I split the rectangle into a left and a right rectangle if the rectangle’s width is greater than it’s height and vice-versa. To generate two sub-rectangles, I simply choose a random point along the $x$-axis in case of a left/right split or along $y$-axis in case of a top/bottom split.
To handle the second pitfall, I defined some padding numbers so that the points I generated were not too close to the current rectangle’s edges. The code for splitting a rectangle goes as follows:
class Rectangle {
split(xPad, yPad) {
if (this.width > this.height) {
var x = randInt(this.min.x + xPad, this.max.x - xPad)
var r1 = new Rectangle(this.min, new Point(x, this.max.y))
var r2 = new Rectangle(new Point(x, this.min.y), this.max)
} else {
var y = randInt(this.min.y + yPad, this.max.y - yPad)
var r1 = new Rectangle(this.min, new Point(this.max.x, y))
var r2 = new Rectangle(new Point(this.min.x, y), this.max)
}
return [r1, r2]
}
}
It takes some time to get the point juggling right but all in all it’s pretty easy; the following illustration might help.

The randInt function simply generates an integer in the $[a, b)$ range, here is it’s definition:
function randInt(min, max) {
return Math.floor(Math.random() * (max - min) + min)
}
As I mentioned the algorithm has to be recursive. This is easy to do, we only have to call the split method on each sub-rectangle. However the issue is to know when to stop. To fix this I simply introduced a depth parameter in the call to the split method; if the current depth is higher than a fixed limit then the recursion stops. Moreover, if a rectangle is too small - i.e. it not wide enough or not tall enough - then the recursion also stops. Finally I added the contouring and the filling of the rectangles into the split method. All in all the code is the following:
var colors = [
'white',
'white',
'white',
'white',
'black',
'red',
'blue',
'yellow'
]
class Rectangle {
split(xPad, yPad, depth, limit, ctx) {
ctx.fillStyle = colors[randInt(0, colors.length)]
ctx.fillRect(this.min.x, this.min.y, this.max.x, this.max.y)
this.draw(ctx)
// Check the level of recursion
if (depth == limit) {
return
}
// Check the rectangle is enough large and tall
if (this.width < 2 * xPad || this.height < 2 *yPad) {
return
}
// If the rectangle is wider than it's height do a left/right split
if (this.width > this.height) {
var x = randInt(this.min.x + xPad, this.max.x - xPad)
var r1 = new Rectangle(this.min, new Point(x, this.max.y))
var r2 = new Rectangle(new Point(x, this.min.y), this.max)
// Else do a top/bottom split
} else {
var y = randInt(this.min.y + yPad, this.max.y - yPad)
var r1 = new Rectangle(this.min, new Point(this.max.x, y))
var r2 = new Rectangle(new Point(this.min.x, y), this.max)
}
// Split the sub-rectangles
r1.split(xPad, yPad, depth+1, limit, ctx)
r2.split(xPad, yPad, depth+1, limit, ctx)
}
}
The colors variable has more whites so that the white color appears more often on the resulting image. To run the code with a canvas we simply have to obtain the canvas’s dimensions, create a rectangle from these dimensions and then call the split method on this initial rectangle.
var c = document.getElementById("doodle")
var ctx = c.getContext("2d")
ctx.beginPath()
ctx.lineWidth = 4
var xPad = Math.floor(c.width * 0.1)
var yPad = Math.floor(c.height * 0.1)
var initialRect = new Rectangle(new Point(0, 0), new Point(c.width, c.height))
initialRect.split(xPad, yPad, 0, 5, ctx)
That’s all there is to it! The full code is available on GitHub. I hope you enjoyed the read!