Recursive polygons with JavaScript

I like modern art, I enjoy looking at the stuff that was made at the beginning of the 20th century and thinking how it is still shaping today’s style. I’m not an expert, it’s just a hobby of mine. I especially like the Centre Pompidou in Paris, it’s got loads of fascinating stuff. While I was going through the galleries it struck me that some of the paintings were very geometrical. In fact they were so geometrical that a machine could have produced them! I’m not talking about artificial intelligence but rather a set of rules that could be given to a programming language. Through a series of blog posts I would like to try to emulate some works with my computer. I realize it’s a waste of time but it’s a good opportunity for me to learn some more JavaScript and refreshen my geometry. I also want to insist on making these drawings random, not deterministic.

The work

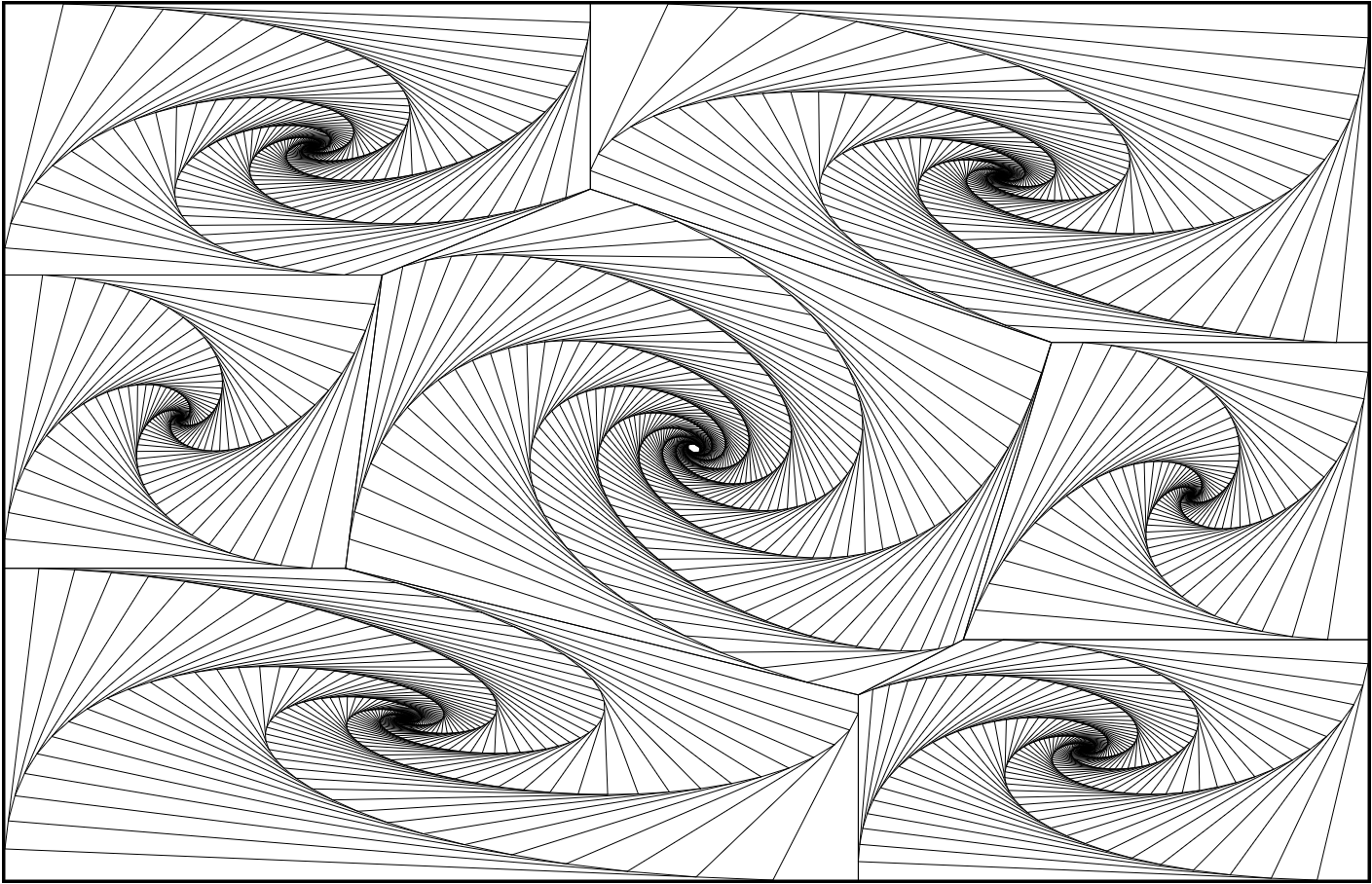
In this post I want to render a doodle I like with a program.

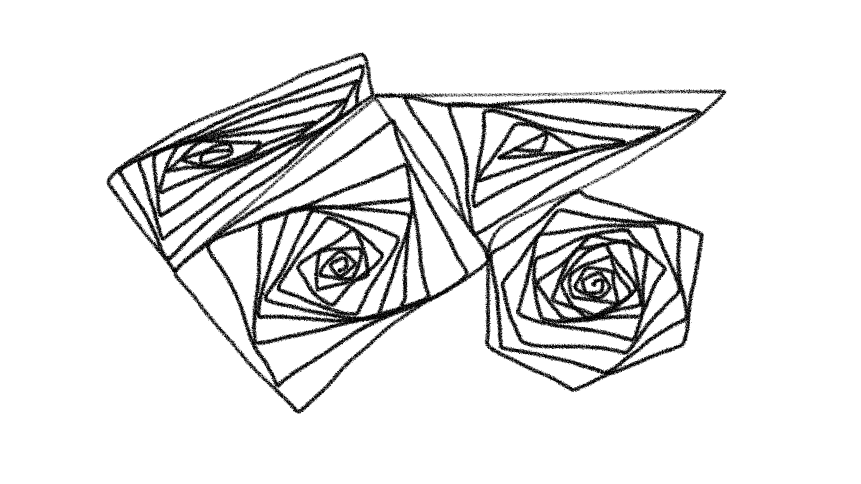
Much like other doodles, it doesn’t make much sense except for it’s “creator”. The idea is to draw a convex polygon where each corner is connected slightly to the right/left of the next one. After a few iterations the polygon starts spiraling down and unexplainable satisfaction stirs in me. Try it for yourself!

The code

The first problem I encountered was how to generate a random convex $n$-sided polygon. At first I coded some rules so that each new side of the polygon defines an interior angle of less than 180 degrees. This proved difficult and not very convincing. My second idea requires an initial step but works wonders.

The intuition I had was that by picking random points on each side of an $n$-sided polygon and joining them, the resulting polygon would also be $n$-sided and convex. It’s a bit hard to explain but it’s easy to convince oneself of this “conjecture”.

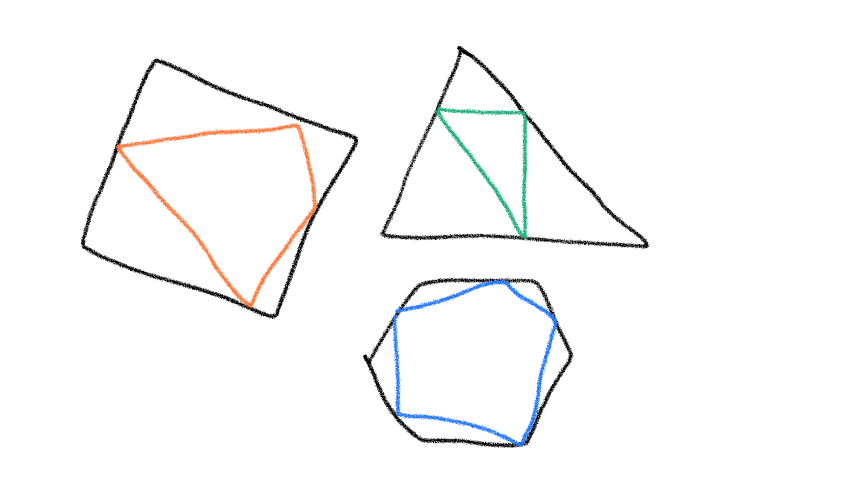
The first objective is thus to create a bounding box into which will fit a random polygon. The characteristics of the bounding box don’t matter because the polygon that it contains will be defined randomly. The only requirement for the bounding box is that it be $n$-sided.

My technique is to use the trigonometric circle. To go around the circle you have to go forward $2\pi$ radians. Hence if you create a list of equivalently distributed proportions of $2\pi$ then you have a list of points.

Because throughout the code I use a lot of geometric points I decided to create a class to make it more readable.

class Point {
    constructor(x, y) {
        this.x = x;
        this.y = y;
    }
}

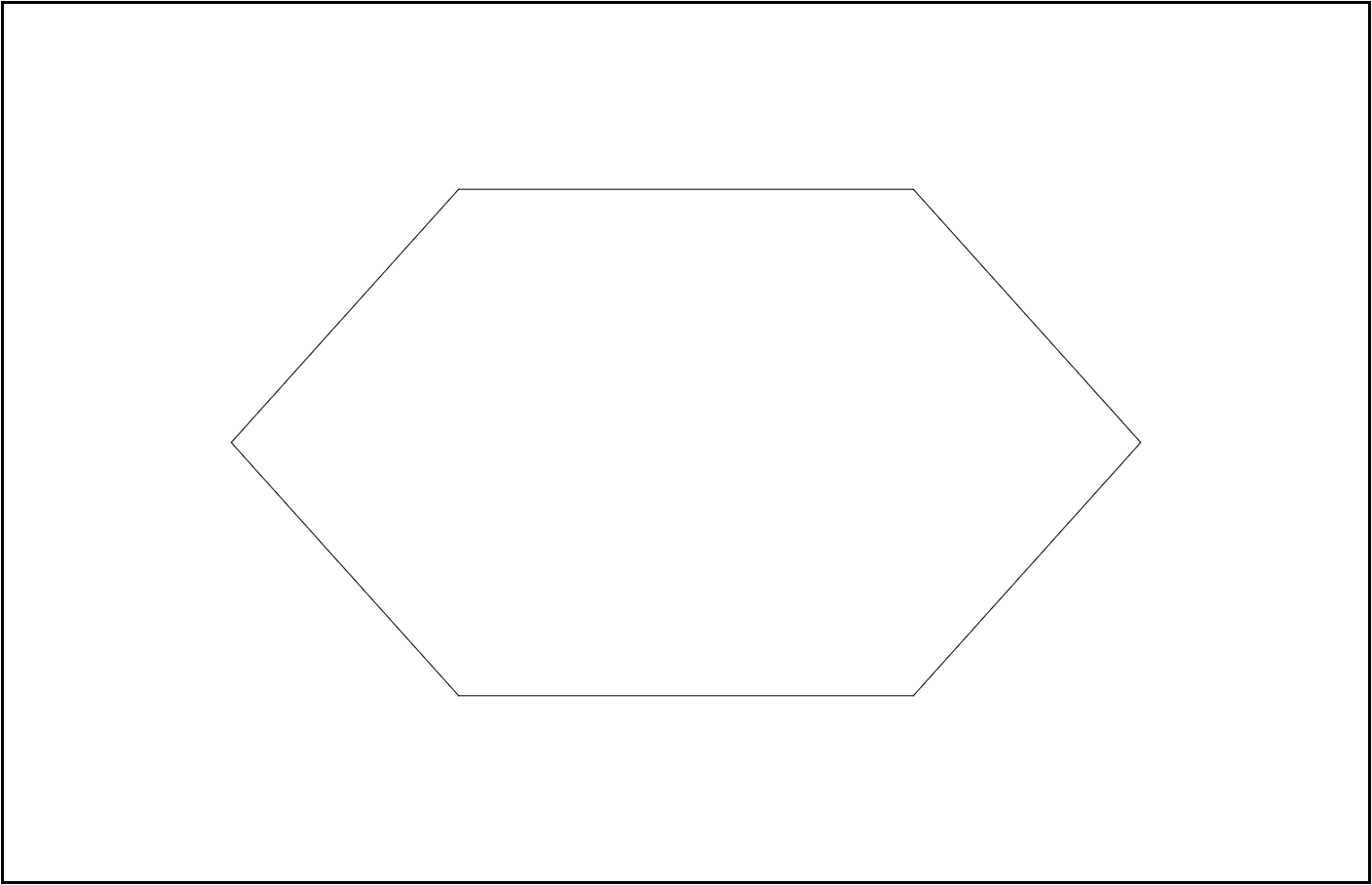
The code for generating a bounding box is not to complicated. To make things more flexible I added parameters so that the trigonometric circle can be an ellipse with a desired width and height.

function createBoundingBox(n, width, height, center) {
    // The bounding box points is generated with the trigonometric circle
    var radians = [];
    for (i = 0; i < n; i++) {
        radians[i] = (i / n) * (2 * Math.PI);
    }
    // Bounding box coordinates
    var box = [];
    // Starting point
    box[0] = new Point(center.x + width * Math.cos(radians[0]), center.y);
    // Complete the bounding box
    for (i = 1; i < n; i++) {
        box[i] = new Point();
        box[i].x = center.x + width * Math.cos(radians[i]);
        box[i].y = center.y + height * Math.sin(radians[i]);
    }
    return box
}

Next for generating a polygon we simple have to iterate through the sides of the bounding box and pick random points to join.

function createConvexPolygon(box) {
    var polygon = [];
    // Complete the polygon
    for (i = 0; i < box.length; i++) {
        polygon[i] = new Point();
        var r = Math.random();
        // Use the modulo operator for cycling through the array
        polygon[i].x = box[i].x + r * (box[(i+1) % box.length].x - box[i].x);
        polygon[i].y = box[i].y + r * (box[(i+1) % box.length].y - box[i].y);
    }
    return polygon
}

I use the modulo operator so that I can join the last point of the polygon to the first one, it avoids adding another instruction after the loop. It’s a bit like using a linked list.

The next step is to draw the outline of the polygon and to start spiraling down. To spiral down, the idea is to choose a random point somewhere in between of the two next points.

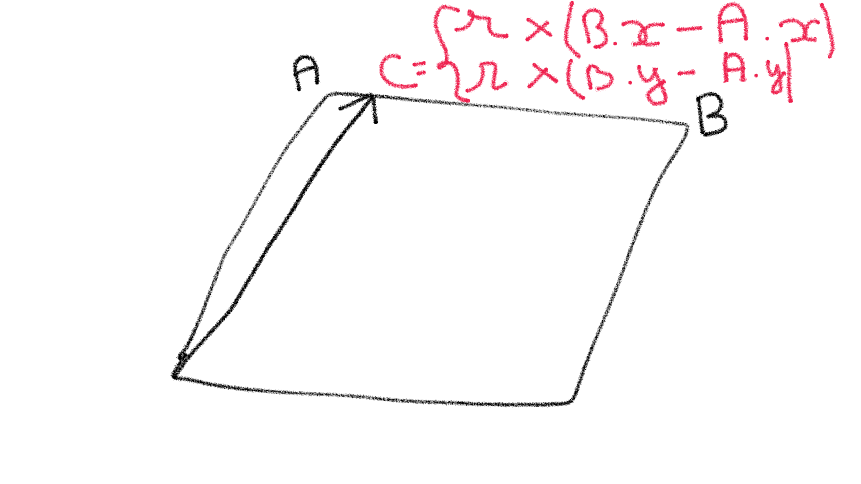
More formally the goal is join each point $p_i$ to a new point in between $p_{i+1}$ and $p_{i+2}$. At each step $i$ we append to the polygon a point such that

$$ x = r \times (x_{i+2} - x_{i+1}) \ y = r \times (y_{i+2} - y_{i+1}) \ 0 < r < 1 $$

function drawPolygon(ctx, polygon) {
    // Draw the outline of the polygon
    ctx.moveTo(polygon[0].x, polygon[0].y);
    for (i = 1; i <= polygon.length; i++) {
        ctx.lineTo(polygon[i % polygon.length].x, polygon[i % polygon.length].y);
    }
    // Go to the end of the polygon
    ctx.moveTo(polygon[polygon.length-1].x, polygon[polygon.length-1].y);
    // Start doodling
    for (i = 0; i < 500; i++) {
        var r = 0.1;
        var x = polygon[i].x + r * (polygon[i+1].x - polygon[i].x);
        var y = polygon[i].y + r * (polygon[i+1].y - polygon[i].y);
        ctx.lineTo(x, y);
        polygon[polygon.length] = new Point(x, y);
    }
    // Go to the end of the polygon
    ctx.moveTo(polygon[0].x, polygon[0].y);
}

And we’re nearly done! I hard coded some polygons so that the rest of the space is filled. I didn’t figure out any obvious property to put it into a loop yet.

The full code is available on GitHub.